中国古代数学的开创性贡献
中国古代数学源远流长,《九章算术》形成完整体系。祖冲之推算圆周率至小数点后七位,刘徽的割圆术和贾宪的杨辉三角展现了古代数学家的智慧。这些成就推动了中国数学发展,也为世界数学史留下重要一笔。

古代数学经典的智慧结晶
中国古代数学著作丰富多样,其中许多经典至今仍具有重要的学术价值。
《九章算术》——中国古代数学的奠基之作
《九章算术》是中国古代最重要的数学著作之一,涵盖了算术、代数、几何等多个领域。它的出现标志着中国古代数学体系的形成,对后世数学发展产生了深远影响。
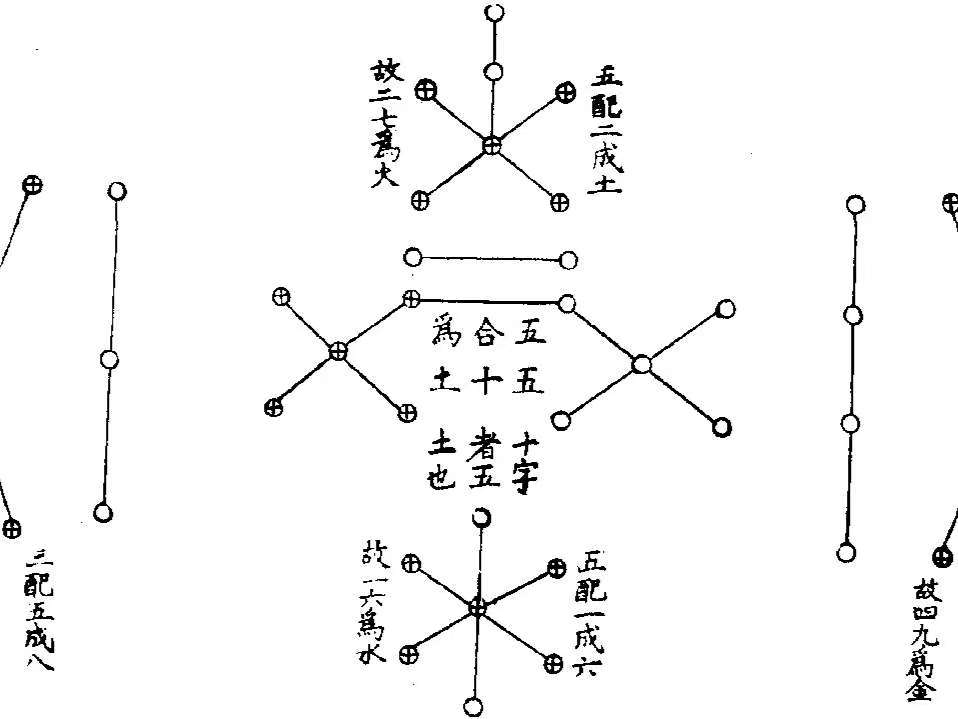
《周髀算经》——天文学与数学的结合
《周髀算经》是中国最早的天文学和数学著作之一,其中包含了勾股定理的早期形式,展现了古代数学与天文学的紧密联系,为后世数学的发展奠定了重要基础。
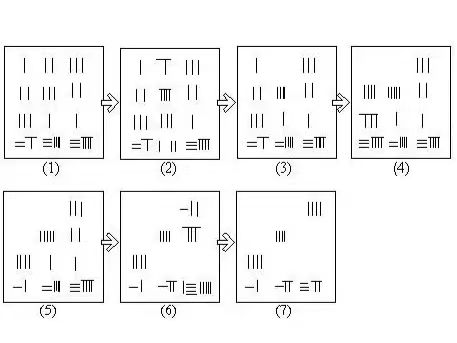
《孙子算经》——实用数学的代表之作
《孙子算经》是中国古代实用数学的杰出代表作,其中记载了许多实际问题的精妙解决方法,如著名的"物不知数"问题,为后世数论研究提供了重要启示。
古代数学家的智慧与成就



祖冲之——圆周率的精确计算
祖冲之是南北朝时期的著名数学家,他首次将圆周率推算至小数点后七位(3.1415926到3.1415927之间),这一成就领先世界近千年。他还提出了"祖率"的概念,为后世数学研究奠定了基础。
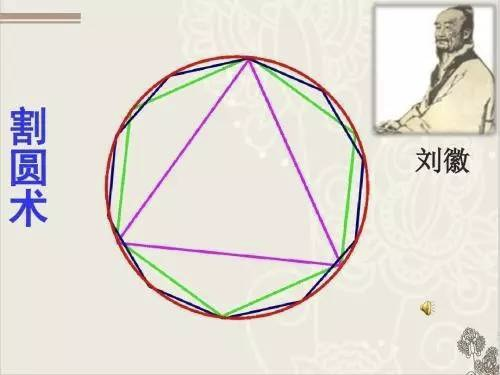
刘徽——割圆术的发明者
刘徽是三国时期的数学家,他发明的割圆术通过不断分割圆的内接多边形来逼近圆周率,为圆周率的计算提供了理论依据。他的方法体现了极限思想的早期萌芽。
贾宪——杨辉三角的奠基人
贾宪是北宋时期的数学家,他提出的"贾宪三角"(后称杨辉三角)是二项式系数的重要表现形式。这一成果不仅在中国数学史上具有重要意义,还为后世组合数学的发展提供了重要工具。
数学家成就时间轴
圆周率计算精度演进
刘徽割圆术公式:
$$ \pi \approx \frac{n \cdot s}{r} \quad (n \to \infty) $$其中 \( n \) 为多边形边数,\( s \) 为边长,\( r \) 为半径
贾宪三角(杨辉三角)
第\( n \)行第\( k \)项表示组合数 \( C(n,k) \),计算公式为:
$$ C(n,k) = \frac{n!}{k!(n-k)!} $$三角性质:
- 每行首末项为1
- 任意数等于肩上两数之和 \( C(n,k) = C(n-1,k-1) + C(n-1,k) \)
- 第\( n \)行和为 \( 2^n \)
古代数学的独特方法与思想
中国古代数学家创造了许多独特的数学方法和思想,这些方法不仅解决了实际问题,还为数学理论的发展提供了重要启示。
中国古代数学的全球影响
中国古代数学成就不仅在国内产生了深远影响,还通过丝绸之路等途径传播到世界各地,为全球数学发展作出了重要贡献。